LeetCode算法题整理（并查集篇）UnionFind

Posted on   |   Updated on | In | | Visitors

1697. Checking Existence of Edge Length Limited Paths

给你一个 n 个点组成的无向图边集 edgeList ，其中 edgeList[i] = [ui, vi, disi] 表示点 ui 和点 vi 之间有一条长度为 disi 的边。请注意，两个点之间可能有 超过一条边 。给你一个查询数组queries ，其中 queries[j] = [pj, qj, limitj] ，你的任务是对于每个查询 queries[j] ，判断是否存在从 pj 到 qj 的路径，且这条路径上的每一条边都 严格小于 limitj 。请你返回一个 布尔数组 answer ，其中 answer.length == queries.length ，当 queries[j] 的查询结果为 true 时， answer 第 j 个值为 true ，否则为 false 。

1
2
3
4
5
输入：n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
输出：[false,true]
解释：上图为给定的输入数据。注意到 0 和 1 之间有两条重边，分别为 2 和 16 。
对于第一个查询，0 和 1 之间没有小于 2 的边，所以我们返回 false 。
对于第二个查询，有一条路径（0 -> 1 -> 2）两条边都小于 5 ，所以这个查询我们返回 true 。

方法一：离线算法+并查集。比赛中没时间做，此题要用并查集。

在线算法，可以用来处理数据流。算法不需要一次性地把所有的 query 都收集到再处理。大家也可以想象成：把这个算法直接部署到线上，尽管在线上可能又产生了很多新的 query，也不影响，算法照常运行。

离线算法则不同。离线算法需要把所有的信息都收集到，才能运行。处理当前 query 的计算过程，可能需要使用之后 query 的信息。

以排序算法为例，插入排序算法是一种在线算法。因为可以把插入排序算法的待排序数组看做是一个数据流。插入排序算法顺次把每一个数据插入到当前排好序数组部分的正确位置。在排序过程中，即使后面源源不断来新的数据也不怕，整个算法照常进行。

选择排序算法则是一种离线算法。因为选择排序算法一上来要找到整个数组中最小的元素；然后找第二小元素；以此类推。这就要求不能再有新的数据了。因为刚找到最小元素，再来的新数据中有更小的元素，之前的计算就不正确了。

按照queries的limit排序，这样我们只需要查看当前的边是否联通来知道是否这条路径上的每条边都小于limit。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:
    edgeList.sort(key=itemgetter(2))

    def union(x, y):
        uf[find(x)] = find(y)

    def find(x):
        uf.setdefault(x, x)
        if x != uf[x]:
            uf[x] = find(uf[x])
        return uf[x]

    uf = {}
    Q = len(queries)
    E = len(edgeList)

    ans = [None] * Q
    j = 0

    for l, i, a, b in sorted(((l, i, a, b) for i, (a, b, l) in enumerate(queries))):
        while j < E and edgeList[j][2] < l:
            x, y, _ = edgeList[j]
            union(x, y)
            j += 1

        ans[i] = find(a)==find(b)

    return ans

1319. Number of Operations to Make Network Connected

最少需要多少步可以将所有的服务器相连。

1
2
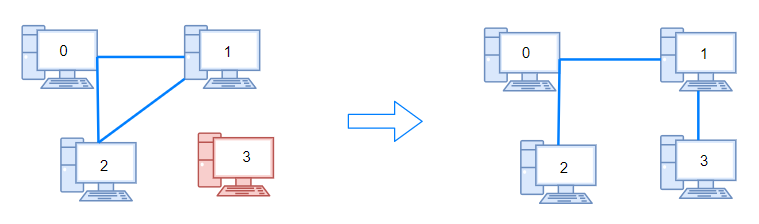
3
Input: n = 4, connections = [[0,1],[0,2],[1,2]]
Output: 1
Explanation: Remove cable between computer 1 and 2 and place between computers 1 and 3.

方法一：dfs. 如果线够，就可以将所有的服务器相连，找到连通器的个数然后-1，就是需要的操作数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def makeConnected(self, n: int, connections: List[List[int]]) -> int:
    if len(connections) < n-1:
        return -1

    g = defaultdict(list)
    for u, v in connections:
        g[u].append(v)
        g[v].append(u)

    seen = set()

    def dfs(i):
        if i in seen:
            return 0
        seen.add(i)
        for j in g[i]:
            dfs(j)
        return 1

    return sum(dfs(i) for i in range(n)) - 1

方法二：并查集。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def makeConnected(self, n: int, connections: List[List[int]]) -> int:
    if len(connections) < n-1:
        return -1        

    uf = list(range(n))
    def union(x, y):
        uf[find(x)] = find(y)

    def find(x):
        if uf[x] != x:
            uf[x] = find(uf[x])
        return uf[x]

    for u, v in connections:
        union(u, v)

    return len({find(i) for i in range(n)}) - 1

1489. Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree

找到最小生成树的关建边和伪关建边。关建边指去掉这条边以后，路径和会增加。伪关建边，因为生成树图不唯一，指有的生成树图中有这条边，有的没有。还有一种是冗余边，指的是必须要去掉的边。分别返回关建边和伪关建边的索引。

1
2
3
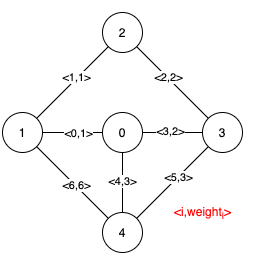
4
Input: n = 5, edges = [[0,1,1],[1,2,1],[2,3,2],[0,3,2],[0,4,3],[3,4,3],[1,4,6]]
Output: [[0,1],[2,3,4,5]]
Explanation: The figure above describes the graph.
The following figure shows all the possible MSTs:

方法一：Union-Find & Kruskal’s 算法。按照Kruskal算法，我们先将所有的边按权重排列。先将所有点边传入得到一个最小生成树的路径和S。再将每条边去掉剩下的边求路径和S1，如果大于S，则说明这是一条关建边；否则它可能是一条伪关建边或者冗余边。然后我们将这条边加到图中，生成一个路径和S2。如果S2和S1相等，则说明是伪关建边。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
def findCriticalAndPseudoCriticalEdges(self, n: int, edges: List[List[int]]) -> List[List[int]]:

    def min_spanning_tree(edges, m_edge=None):

        uf = list(range(n))
        def union(x, y):
            uf[find(x)] = find(y)

        def find(x):
            if uf[x] != x:
                uf[x] = find(uf[x])
            return uf[x]

        edges = [(w, u, v) for u, v, w in edges]
        heapq.heapify(edges)
        cnt, ans = 1, 0
        if m_edge:
            uu, vv, ww = m_edge
            cnt += 1
            ans += ww
            union(uu, vv)
        else:
            uu, vv, ww = -1, -1, -1
        while cnt < n:
            if not edges:
                return inf
            d, u, v = heapq.heappop(edges)
            if u==uu and v == vv:
                continue
            if find(u) != find(v):
                ans += d
                cnt += 1
                union(u, v)
        return ans

    res = [[], []]
    mm = min_spanning_tree(edges)
    for i in range(len(edges)):
        cur = min_spanning_tree(edges[:i]+edges[i+1:])
        if cur == mm:
            # 伪关键边或冗余边
            include = min_spanning_tree(edges, edges[i])
            if include == mm:
                res[1].append(i)
        else:
            res[0].append(i)
    return res

方法二：待定

1579. Remove Max Number of Edges to Keep Graph Fully Traversable

找到能使Alice，Bob任意节点都能遍历完整图的最多删除的边的条数。

1
2
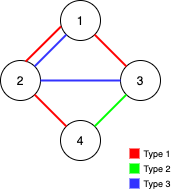
3
Input: n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
Output: 2
Explanation: If we remove the 2 edges [1,1,2] and [1,1,3]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.

方法一：贪心+并查集。优先保留类型3的边。注意类型3的边也可能增加结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class UF:
    def __init__(self, n):
        self.uf = list(range(n+1))
        self.n = n

    def union(self, x, y):
            self.uf[self.find(x)] = self.find(y)

    def find(self, x):
        if self.uf[x] != x:
            self.uf[x] = self.find(self.uf[x])
        return self.uf[x]

    def all_connected(self):
        return len({self.find(i) for i in range(1, self.n+1)}) == 1

class Solution:
    def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:
        self.res = 0
        edges_3 = ([t, u, v] for t, u, v in edges if t==3)
        edges_2 = ([t, u, v] for t, u, v in edges if t==2)
        edges_1 = ([t, u, v] for t, u, v in edges if t==1)

        uf = UF(n)
        def connect(uf, edges):
            for _, u, v in edges:
                if uf.find(u) == uf.find(v):
                    self.res += 1
                else:
                    uf.union(u, v)
            return uf, uf.all_connected()

        cp_uf, _ = connect(uf, edges_3)
        cp_uf = copy.deepcopy(uf)
        _, connected = connect(uf, edges_2)
        if not connected: return -1
        _, connected = connect(cp_uf, edges_1)
        if not connected: return -1
        return self.res